TABLE INDEX
A table index is a replica of a subset of a table’s attributes that are organized and/or sorted for efficient access using those attributes.The DBMS ensures that the contents of the table and the index are logically synchronized.
索引让数据在数据库中的查询更加的高效,DBMS负责使索引和实际内容同步。

DBMS的工作是选择最优的索引去执行查询,这就带来一个需要权衡的问题——索引越多查询越高效但是相对的维护成本(Maintenance Overhead)和存储成本(Storage Overhead) 就会相应的提高。
B-TREE FAMILY
B-树家族。
重点了解B+树。

(B树虽然是一个平衡树(balance),但B树的B不是balance的缩写,到底代表什么还存疑)
B+TREE

B+树是一个自平衡树的数据结构,顺序的存储数据,并且将查询,顺序访问,插入和删除的时间复杂度基本控制在O(log n)。
- 是二叉搜索树的推广,因为它可以有超过两个的孩子节点。
- 它针对系统和存储之间的大块数据读写进行了特别的优化。
B+TREE PROPERTIES

B+树是一个多叉搜索树,有以下特性:
- 他完美平衡
- 除了根节点都至少半满
- k个值会把一个节点分为k+1部分。
B+TREE EXAMPLE
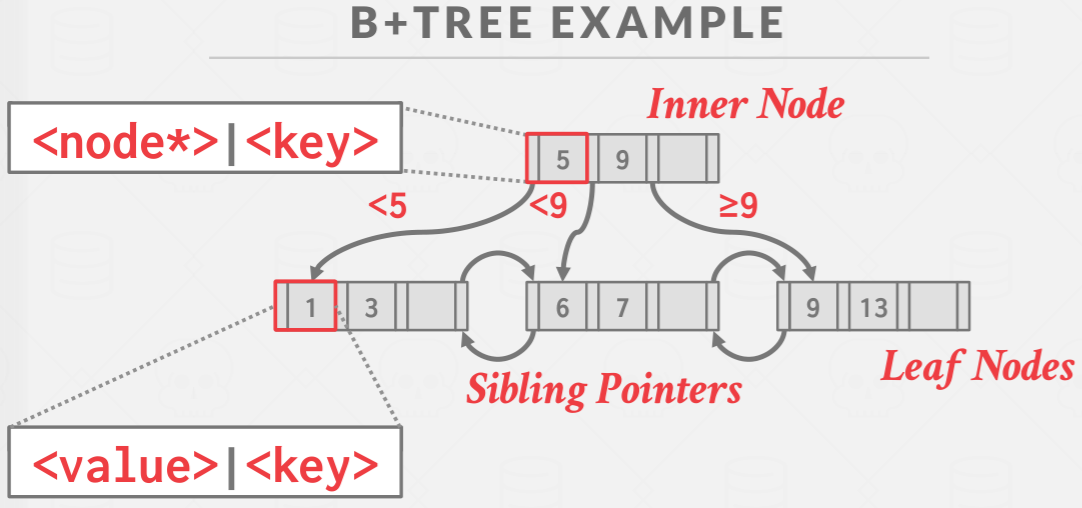
上图是一个小例子,能够发现B+树底层是能够双向访问的,这在多线程的时候有可能会造成死锁问题。这在后面讲解B+树多线程的章节也会对原因进行讲解。
B+‘s CRUD
可以说B+树的增删改查的特性和它的组织形式是密不可分的。每次做改动之后都要符合他的结构特性,所以也没什么好说的。
B+树的一些应用扩展
二级索引 && 记录迁移
如果二级索引的叶子节点直接指向的是对应数据的指针,那么在发生增删的时候结构发生变化二级索引就需要进行重构,这不仅是一项开销非常大的方法,而且还难以保证数据的同步。
解决办法:
辅助索引的叶子节点存主键的值列表,这种关系的固定的不会改变的,一两个数据的增删不会造成整个树的重构。
这就避免了由于重构导致变化而二级索引需要跟着重构的带来的开销。现需要在辅助索引上查到需要的主键列表然后再去主键索引上去查找对应的数据。
这样虽然降低了查询时候的一点效率,但是跟频繁的重构比起来还是难以感知的😃。
字符串索引
尽力一个B+树的字符串索引有两个问题:
- 字符串一般都是变长的,这很难解决
- 因为字符串可能会很长,所以扇的出度会降低,相应的树高会变高。
对应的解决办法有以下两点:
- 灵活的出度。每个扇的出度并不是简单固定的,根据这个扇的字符串所用的空间进行灵活的调整。
- 前缀压缩。只用存储到不一样的第一位,能够分辨就够了。
例如,如果我们有一个名称索引,那么非叶节点上的键值可以是名称的前缀;如果它分离的两个子树中最接近的值分别是“Silas”和“Silver”,那么在非叶节点存储“Silb”而不是完整的“Silberschatz”就足够了。这就是前缀压缩
批量加载B+树索引
前面我们知道B+树的插入操作开销非常的大,一定程度上这个插入的开销和树的高度是成正比的。所以树的高度一般最多被控制在5,对于大型项目也是这样的。
正因为如此,加入现在有100万条数据需要插入,每条数据光是I/O都需要很长的时间,更不用说插入之后B+树重构的时间。
现在有一种优化的方法,将需要插入的大量数据进行排序后按照B+树的方法构建索引后将这颗构建的树merge到原来的B+树中,这样做有以下几个好处:
- 在多线程方面具有优势
- 在构建的时候会产生更少的I/O.
- 叶子节点会按顺序进行排序。
下面是一个用chatgpt写出来的一个b+树的小demo,用来窥探一下具体实现是很有帮助的。
#include <iostream>
#include <vector>
#include <algorithm>
const int ORDER = 3; // B+树的阶数
// B+树节点
template <typename Key, typename Value>
struct BPlusTreeNode {
bool isLeaf;
std::vector<Key> keys;
std::vector<Value> values;
BPlusTreeNode* parent;
BPlusTreeNode* next; // 用于叶子节点的连接
};
// B+树
template <typename Key, typename Value>
class BPlusTree {
public:
BPlusTree() : root(nullptr) {}
void insert(const Key& key, const Value& value) {
if (root == nullptr) {
root = new BPlusTreeNode<Key, Value>();
root->isLeaf = true;
root->keys.push_back(key);
root->values.push_back(value);
} else {
insertHelper(root, key, value);
}
}
Value search(const Key& key) const {
return searchHelper(root, key);
}
void print() const {
printHelper(root, 0);
}
private:
BPlusTreeNode<Key, Value>* root;
void insertHelper(BPlusTreeNode<Key, Value>* node, const Key& key, const Value& value) {
if (node->isLeaf) {
insertIntoLeaf(node, key, value);
} else {
int i = 0;
while (i < node->keys.size() && key > node->keys[i]) {
i++;
}
insertHelper(node->children[i], key, value);
}
}
void insertIntoLeaf(BPlusTreeNode<Key, Value>* node, const Key& key, const Value& value) {
auto it = std::lower_bound(node->keys.begin(), node->keys.end(), key);
int index = it - node->keys.begin();
node->keys.insert(it, key);
node->values.insert(node->values.begin() + index, value);
if (node->keys.size() > ORDER - 1) {
splitLeaf(node);
}
}
void splitLeaf(BPlusTreeNode<Key, Value>* node) {
BPlusTreeNode<Key, Value>* newLeaf = new BPlusTreeNode<Key, Value>();
newLeaf->isLeaf = true;
int splitIndex = (ORDER - 1) / 2;
newLeaf->keys.assign(node->keys.begin() + splitIndex, node->keys.end());
newLeaf->values.assign(node->values.begin() + splitIndex, node->values.end());
node->keys.resize(splitIndex);
node->values.resize(splitIndex);
newLeaf->next = node->next;
node->next = newLeaf;
insertIntoParent(node, newLeaf->keys[0], newLeaf);
}
void insertIntoParent(BPlusTreeNode<Key, Value>* left, const Key& key, BPlusTreeNode<Key, Value>* right) {
if (root == left) {
BPlusTreeNode<Key, Value>* newRoot = new BPlusTreeNode<Key, Value>();
newRoot->keys.push_back(key);
newRoot->children.push_back(left);
newRoot->children.push_back(right);
left->parent = newRoot;
right->parent = newRoot;
root = newRoot;
} else {
BPlusTreeNode<Key, Value>* parent = left->parent;
auto it = std::lower_bound(parent->keys.begin(), parent->keys.end(), key);
int index = it - parent->keys.begin();
parent->keys.insert(it, key);
parent->children.insert(parent->children.begin() + index + 1, right);
right->parent = parent;
if (parent->keys.size() > ORDER - 1) {
splitInternal(parent);
}
}
}
void splitInternal(BPlusTreeNode<Key, Value>* node) {
BPlusTreeNode<Key, Value>* newInternal = new BPlusTreeNode<Key, Value>();
int splitIndex = (ORDER - 1) / 2;
Key upKey = node->keys[splitIndex];
newInternal->keys.assign(node->keys.begin() + splitIndex + 1, node->keys.end());
newInternal->children.assign(node->children.begin() + splitIndex + 1, node->children.end());
node->keys.resize(splitIndex);
node->children.resize(splitIndex + 1);
for (auto child : newInternal->children) {
child->parent = newInternal;
}
insertIntoParent(node, upKey, newInternal);
}
Value searchHelper(BPlusTreeNode<Key, Value>* node, const Key& key) const {
if (node == nullptr) {
return Value(); // 返回默认值表示未找到
}
int i = 0;
while (i < node->keys.size() && key > node->keys[i]) {
i++;
}
if (node->isLeaf) {
if (i < node->keys.size() && key == node->keys[i]) {
return node->values[i];
} else {
return Value(); // 返回默认值表示未找到
}
} else {
return searchHelper(node->children[i], key);
}
}
void printHelper(BPlusTreeNode<Key, Value>* node, int level) const {
if (node != nullptr) {
std::cout << "Level " << level << ": ";
for (int i = 0; i < node->keys.size(); ++i) {
std::cout << node->keys[i] << " ";
}
std::cout << std::endl;
if (!node->isLeaf) {
for (auto child : node->children) {
printHelper(child, level + 1);
}
}
}
}
};
int main() {
BPlusTree<int, std::string> bPlusTree;
// 插入示例
bPlusTree.insert(10, "Value10");
bPlusTree.insert(20, "Value20");
bPlusTree.insert(5, "Value5");
bPlusTree.insert(6, "Value6");
bPlusTree.insert(12, "Value12");
bPlusTree.insert(30, "Value30");
bPlusTree.insert(7, "Value7");
bPlusTree.insert(17, "Value17");
bPlusTree.insert(25, "Value25");
// 打印B+树
bPlusTree.print();
// 搜索示例
int keyToSearch = 12;
std::
多线程的B+树
Locks&&Latches
==两者区别==

- 个人认为是存在的维度不太一样。locks适用于宏观方面的,latches则是细致入微的。
- (剩下的还待总结、、、体会确实没有那么的深刻😀),不过可以参考chatgpt说的。

==读模式和写模式==

- 读模式比较随意,因为不涉及修改所以谁读都无所谓,只是在读的时候不能修改
- 写模式因为涉及到修改,所以只有唯一的一个线程能够进行写。
 这张图可以解释latch的正常运行的逻辑。
这张图可以解释latch的正常运行的逻辑。
Latches的实现
==方法一==

 这三种“mutex”有何区别。
这三种“mutex”有何区别。

==方法二==

- 允许多线程读,读的时候如果有写🔒需要让写锁等待,之后要用公平的算法平衡,防止某个线程饿死。
- 可以基于自旋锁实现。
Latches的应用
==hash table latches==

- 因为哈希表的搜索方向是朝向同一个方向,在搜索的时候只涉及到一个数据页或行
- 不会发生搜索冲突的现象,因此不可能发生死锁
- 在resize哈希表的时候在header page上🔒一下,就能保证整个hash表的写锁。
==实现==

- 在每个页或者每一行上加上这种细粒度的锁自然是有助于效率的提升
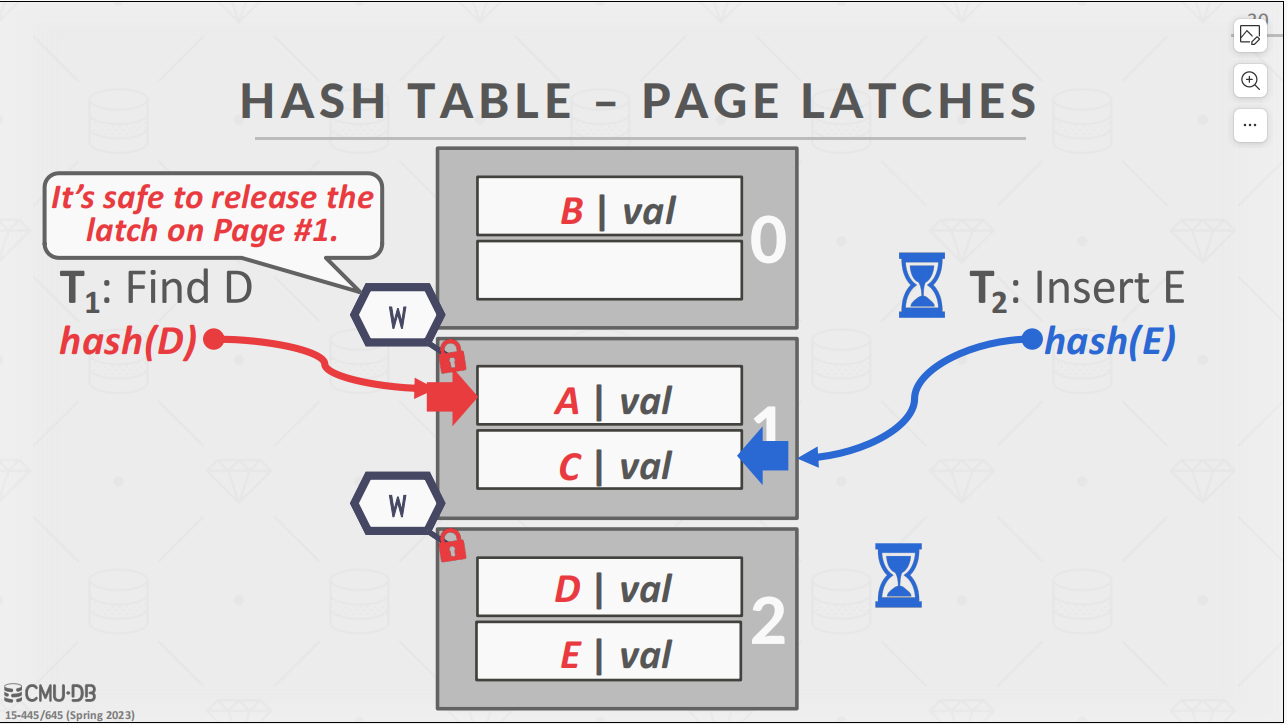
- 在搜寻到下一页的时候上一页处于什么状态已经没有任何关系了,所以可以放心的释放锁

- 这是另一种粒度更细的锁,在每一行数据上加锁,搜索到下一行就给上一行解锁。
b+ tree latches
==螃蟹锁==



- 在读的时候:当获取到下一个page的读锁之后就可以释放当前page的读锁。
- 在写的时候:一直递归向下获取写锁,直到碰到一个page是处于安全状态的,就可以释放所有父节点的写锁。(悲观锁)
- 在写的时候:先假设一路上的节点都是处于安全状态的,如果发现有不安全的那么就推到按照悲观锁的方法再来一遍。